English
Zobacz więcej:
- dla uczniów szkół podstawowych: oij.edu.pl/start/
- dla uczniów szkół średnich: oi.edu.pl/l/jak_zaczac/
Zadanie Karty [B] (kar)
Cards [B]
Memory limit: 32 MB
Alice nad Bob have found a few decks of cards at the attic. Some of them were very dusty, some incomplete, and some contained strange honor cards that cannot be found among regular playing cards. However, all cards had one characteristic in common: they were either black or red. Alice and Bob are very creative children. They decided to use all the cards they have found and play the following game.
In the beginning of the game children shuffle all the cards.
Afterwards, they play the cards one by one from the top of the deck onto
the table.
If the first played card is black or some sequence of consecutively played black
cards is not immediately preceded by a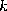 
times longer sequence of
consecutive red cards, then Alice wins the game.
In the opposite case, after all cards have been played, Bob wins the game.
Alice would like to find out what is her chance of winning, so she is
wondering for how many arrangements of cards that could be a result
of shuffling the initial deck she wins with Bob.
We assume that all cards of the same colour are indistinguishable.
Alice has recently heard about the Chinese remainder theorem, so it is
sufficient for her to know the result modulo given prime number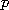 
.
Input
The first and only line of the standard input contains four integers
, 
, 
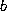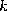, and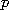 
(
, 
, 
)
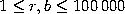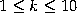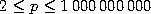separated by single spaces.
Number 
denotes the number of red cards in the deck, whereas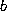 
-
the number of black cards.
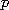is a prime number.
Output
The first and only line of the standard output should contain the remainder
of division by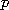 
of the number of arrangements of cards consisting of
red cards and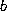 
black cards, for which Alice wins the game.
Example
For the input data:
4 2 1 17
the correct result is:
6
Explanation of the example. In this case Alice wins if either the first card is black or some sequence of consecutive black cards is immediately preceded by a smaller number of consecutive red cards. Let R denote a red card, and B - a black card. These are the arrangements of cards for which Alice wins (the first letter in each of them denotes the card from the top of the deck): BBRRRR, BRBRRR, BRRBRR, BRRRBR, BRRRRB, and RBBRRR.
Task author: Lukasz Bieniasz-Krzywiec.